关于信息论的一些基础常识

Contents

1. 1. Definitions
   1. 1.0.1. 熵（Entropy）
   2. 1.0.2. 互信息（Mutual Information）

2. Commonly-used Properties

1. 2.0.1. Jensen不等式（Jensen Inequality）
2. 2.0.2. 熵和互信息的一些性质（由相对熵的性质引出）（Derived Properties）
3. 2.0.3. 关于条件(conditioning)的影响
4. 2.0.4. 数据处理不等式（Data Processing Inequality）

3. End

这是一些关于信息论（Information Theory）的基本知识 (几乎是常识) 的笔记。我在这里写下来，这样当我忘记它们时，我在这个笔记中迅速取得思路。

Reference: Cover, Thomas M. Elements of information theory (Chapter 2). John Wiley & Sons, 1999.

Definitions

熵（Entropy）

给定一个变量 ，取值自，它的熵被定义为:

$$H(X)=\sum_{x\in\mathcal{X}} p(x) \log\frac{1}{p(x)}=-\sum_{x\in\mathcal{X}} p(x)\log p(x)$$

• 直观理解：可以将想象为某种长度度量，出现概率越小的话，需要用来“编码”的“长度”就需要越长。那么熵就是这个变量长度的期望。
• 所以熵越大，不确定性越大。
• 注意到我们约定.
• 如果log的底是2，那么熵的单位是bits；如果log的底是e的话，则是nats
• 熵是非负的（注意到）.

关于记号：通常用大写表示随机变量，而小写表示具体某个取值。

联合分布的熵与边际分布熵的关系：

$$\begin{align*}H(X,Y) &=-\sum p(x,y)\log p(x,y)\\ &=-\sum p(x)p(y\mid x)\log p(x)p(y\mid x)\\ &=-\sum p(x)\log p(x)+\sum p(y\mid x)\log p(y\mid x)\\ &=H(X)+H(Y\mid X)\\ &=H(Y)+H(X\mid Y)\end{align*}$$

互信息（Mutual Information）

给定变量的两个不同的分布和，他们之间的相对熵（KL散度）定义为：

$$D(p\mid\mid q)=\sum_{x\in\mathcal{X}} p(x)\log\frac{p(x)}{q(x)}$$

两个变量的互信息则定义为：

$$I(X;Y)=D(p(x,y)\mid\mid p(x)p(y))$$

• 注意到，，且
• 两个变量的互信息是由他们的联合分布决定的

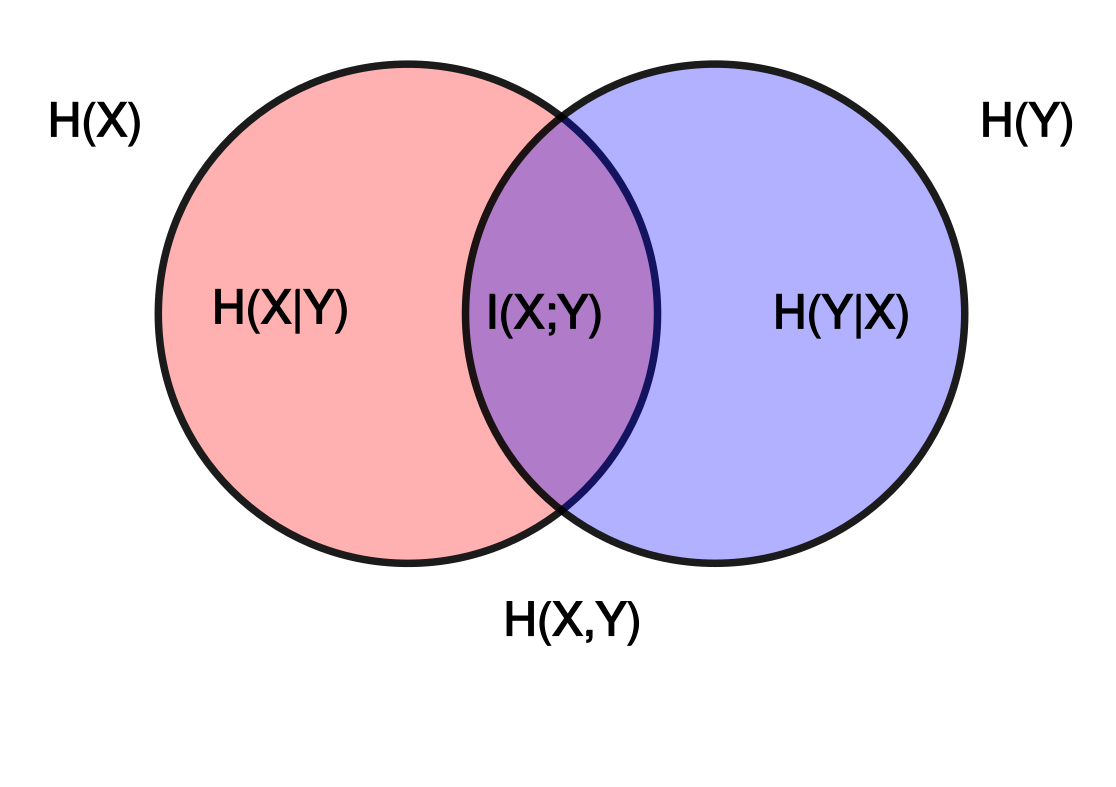
注意到互信息和熵之间的关系：

$$\begin{align*}I(X;Y) &=\sum_{x\in\mathcal{X},y\in\mathcal{Y}}p(x,y)\log\frac{p(x,y)}{p(x)p(y)}\\ &=\sum p(x,y)\log\frac{p(x)p(y\mid x)}{p(x)p(y)}\\ &=\sum p(x,y)\log p(y\mid x)-\sum p(x,y)\log p(y)\\ &=-H(Y\mid X)+H(Y)=-H(X\mid Y)+H(X)\\ &=H(X)+H(Y)-H(X,Y)\end{align*}$$

注意到最后一步实际上是全概率公式，即

Commonly-used Properties

Jensen不等式（Jensen Inequality）

回忆一下上凸函数（concave）和下凸函数（convex）的定义，也就是若由两个点，有

$$f(\lambda x_1+(1-\lambda)x_2)\le \lambda f(x_1)+(1-\lambda)f(x_2)$$

上面这个是下凸函数，如果是大于等于，则相反；并且，其中等式成立当且仅当=1或0的情况，称之为严格的下/上凸.

常用的是如下表达，即：

$$Ef(X)=\sum p(x)f(x)\le f(EX)=f(\sum p(x)x)$$

即下凸函数的值的期望是小于等于期望的值的；并且如果是严格的，等式成立说明变量是个常量。

信息论里常用到如下对于log-sum函数的下凸性（convexity）的结论：

$$\sum a_i\log\frac{a_i}{b_i}\ge (\sum a_i \log\frac{\sum a_i}{\sum b_i})$$

其中，和是非负的数；等式成立当且仅当. 对应到概率，可以理解为等式成立当且仅当两个概率分布是相等的。证明见书中定理2.7.1.

注意到，如果其中和是两个关于函数，等式成立说明，即某个关于t的函数。

熵和互信息的一些性质（由相对熵的性质引出）（Derived Properties）

关于互信息的性质：

• (non-negativity of relative entropy) 相对熵是非负的；

  利用log函数的上凸性有：

  $$\begin{align*} D(p\mid\mid q) &=\sum p(x)\log\frac{p(x)}{q(x)}\\ &\ge -\log \sum p(x)\frac{q(x)}{p(x)}=0 \end{align*}$$

• (zero relative entropy leads to equality) 如果相对熵等于0，则说明两个分布相同（注意到Jensen不等式相等的条件）。

• (non-negativity of mutual information) 所以，互信息也是非负的。
• (zero mutual information leads to independence) 所以互信息等于0，则说明，即两个分布独立

关于熵的性质：

• (maximum of entropy) 熵有一个最大值，即；这就是服从均匀分布的情况：

  $$\log|\mathcal{X}|-H(X)=\sum p(x)\log \frac{p(x)}{1/log|\mathcal{X}|}=D(p||u)\ge 0.$$

• (conditioning never decrease entropy) 添加条件不会降低熵，即（很符合直觉，多知道东西怎么会降低“信息量”呢？）:

  $$H(X)-H(X\mid Y)=I(X;Y)\ge 0$$

  注意互信息无此结论，因为互信息刻画的是相关性，这会随着已知条件的变化而变化

• (inequality between joint and marginal entropy) 边际分布的熵之和大于等于联合分布的熵，即,

  $$H(X)+H(Y)-H(X,Y)=I(X;Y)\ge 0.$$

  并且可以看出，等式成立当且仅当和独立。

• (convexity of relative entropy) 相对熵关于是下凸的（convex），证明利用log-sum函数的下凸性：

  $$\begin{align*} \sum D(p_i||q_i)&=\sum_i (\sum_x p_i(x)\log\frac{p_i(x)}{q_i(x)})\\ &\ge \sum_x (\sum_i p_i(x)\log\frac{\sum_i p_i(x)}{\sum_i q_i(x)})=D(\sum p_i||\sum q_i)\\ \end{align*}$$

  一定要注意凸性是关于什么成立的。

• (concavity of entorpy) 根据上面的结论，再结合，所以熵是上凸的（concave）。

  (convexity/concavity of mutual information) 互信息并没有如此好的凸性，但若视，则互信息关于前者上凸（固定），而关于后者p(y\mid x)下凸（固定）。感觉这个结论不是很有用，证明见定理2.7.4。

wiki上有两个很直观的图，可以参考（注意可正可负可零）：

关于条件(conditioning)的影响

关于独立性，需要注意到：

• 边际分布独立和条件独立并无关系，即和独立，但并不意味着和独立；
• 并且，若分别与和独立，也不意味着和独立；除非是和独立。

类似有，添加条件，关于互信息的变化并没什么结论，互信息即可能增大，也可能减少，还可能不变。

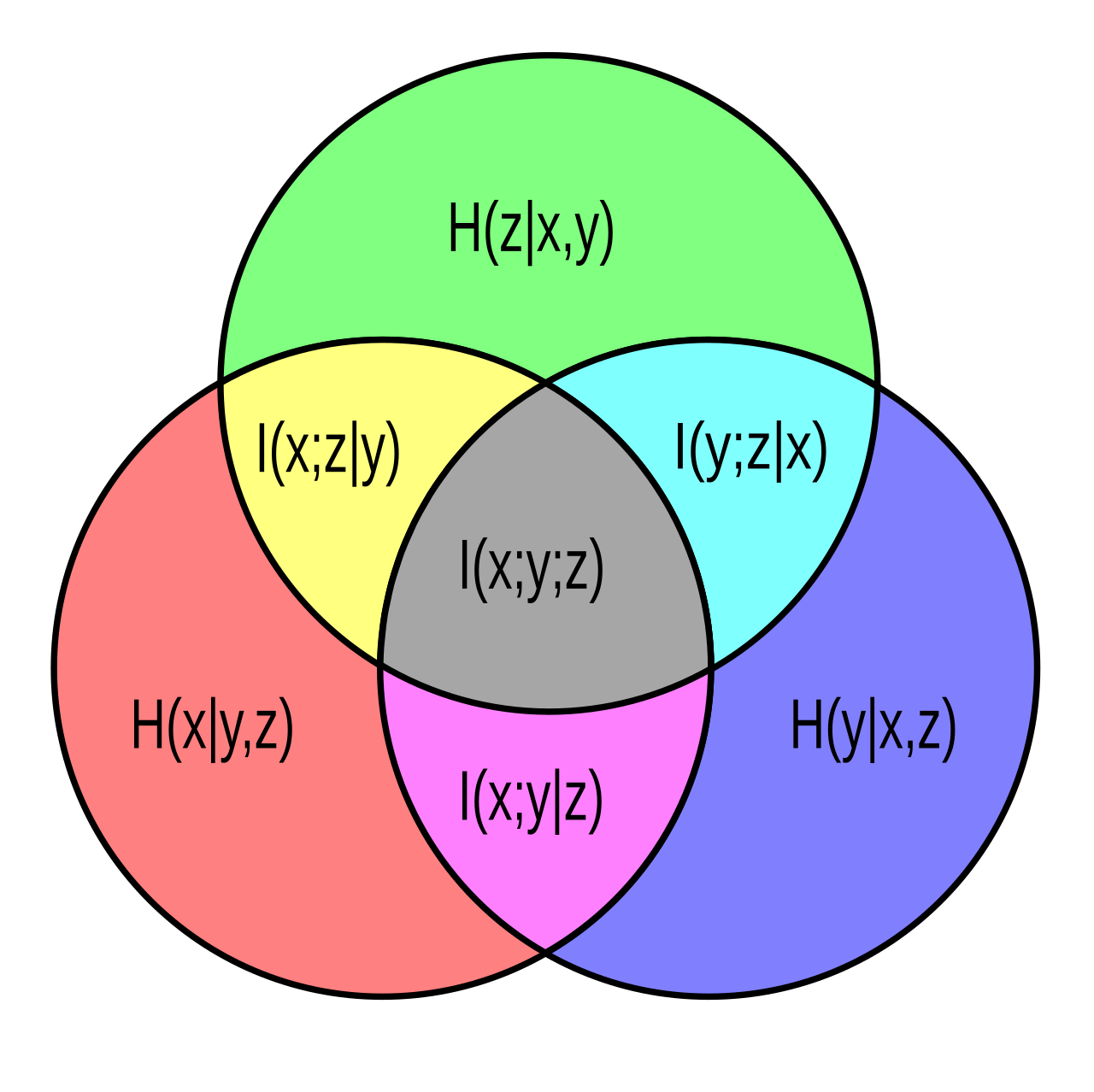
添加条件对于互信息的变化，称为交互信息(Interaction Information)，即.

可以直观理解添加条件之后，互信息变化的意义：

• ，即交互信息为正，这说明某种程度上“排除”了和之间的关联。直观上可以理解为与、中某一个有关联，导致的出现能够解释其中一个，使得和之间的依赖性降低。例如发生车祸，关于驾驶员主观故意和车祸之间的关系，发现汽车刹车失灵，那么上面那个例子的关系就减弱了。
• ，即交互信息为负，这说明某种程度上“支持”了和之间的关联。直观上可以理解为Z与X和Y有某种共同的关联，导致成为和之间有关系的信号。例如，发现有酒味，那么这种关系就增强了。

注意到交互信息为零，即，并不能说明其中一个变量和其余俩独立。

数据处理不等式（Data Processing Inequality）

这也是一个极其常用的不等式。

考虑三个变量的关系：，若（即），则有：

$$I(X;Y)\ge I(X;Z).$$

这个不等式说明数据处理只会“掉”输入的信息，不会“添”输入的信息。

注意到这三个变量之间的关系，是知道了仅仅需要由决定，即已知的情况下，和独立（马尔科夫链），证明就需要利用这个性质：

$$\begin{align*}I(X;Y,Z)&=H(Y,Z)-H(Y,Z\mid X)\\ &=H(Y)+H(Z\mid Y)-(H(Y\mid X)+H(Z\mid Y, X))\\ &=I(X;Y)+I(Z;X\mid Y)=I(X;Z)+I(Y;X\mid Z).\end{align*}$$

三个变量之间关系说明，所以:

$$I(X;Y)=I(X;Z)+I(Y;X\mid Z)\ge I(X;Z).$$

这里可以看出，等式成立的条件是。这有什么实际意义呢？比如Z完全没有丢失Y的信息这种情况，于是知道就能确定，于是当然就和没关系了。

注意到上面的式子，还引出另一个结论，即。这说明条件只能减弱和之间的关系，直观上可以理解为因为能够含有的信息，使得和之间的依赖能够降低。

End

上面总结了一些常用的熵和互信息的基础知识，还有如Fano Inequality等知识没有介绍，需要时可以查阅原书。